Kadane’s Algorithm (카데인 알고리즘)

https://leetcode.com/problems/maximum-subarray/

 

위의 문제는 전체 배열에서의 최대 부분합을 구하는 문제이다. Brute Force 방식으로 문제를 어렵지 않게 해결할 수 있지만, 카데인 알고리즘을 이용하면 O(N)으로 문제를 해결할 수 있다.

문제 예시 주어진 배열 A를 [1,-2,3,5,-4,2,5] 라고 했을 때,Maximum Subarray는 [3,5,-4,2,5] 이며, 결과값은 부분 배열의 합인 11 이다.

Brute Force : O(N²)

Brute Force 방식은 가능한 모든 부분 배열의 합을 구하고 이에 대한 최대값을 구하는 것이다. A[0]부터 시작해서 A[0]에서 가질 수 있는 모든 부분합을 구한다. 이 과정을 A[1], A[2], A[3] ….. A[n] 까지 반복한다.
각 인덱스의 최대 부분합을 maxIndex[i]라고 했을 때, 결과값은 아래와 같다.

결과값 : Math.max(maxIndex[0], maxIndex[1], …. , maxIndex[n])

 

전체 배열을 한번 순회하고, 그 안에서 인덱스 별로 한번씩 더 순회하기 때문에 시간복잡도는 O(N²)이다. 하지만 카데인 알고리즘을 이용하면 O(N) 시간 복잡도로 문제를 해결할 수 있다.

Dynamic Programming

카데인 알고리즘은 다이나믹 프로그래밍을 적용한 방식이다. 다이나믹 프로그래밍은 무엇일까?

다이나믹 프로그래밍 (동적 계획법) 동적 계획법의 원리는 매우 간단하다. 일반적으로 주어진 문제를 풀기 위해서, 문제를 여러 개의 하위 문제(subproblem)로 나누어 푼 다음, 그것을 결합하여 최종적인 목적에 도달하는 것이다. 각 하위 문제의 해결을 계산한 뒤, 그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 그것을 간단하게 해결할 수 있다. 이러한 방법으로 동적 계획법은 계산 횟수를 줄일 수 있다. 특히 이 방법은 하위 문제의 수가 기하급수적으로 증가할 때 유용하다. (출처: 위키백과)

 

다이나믹 프로그래밍의 핵심은 큰 문제를 작은 문제로 쪼개어 해결하고, 한번 풀었던 문제는 어딘가에 저장해두었다가 반복하여 풀지 않는 것이다.

Kadane’s Algorithm : O(N)

다이나믹 프로그래밍에 대한 개념을 새겨둔채로, 최대 부분합 문제의 개념부터 다시 생각해보자. 전체 배열이 주어졌고, 우리는 부분 배열이 가질 수 있는 부분합들 중에서 최대 부분합을 구해야 한다.

이 문제를 O(N)으로 풀기 위한 핵심은 각각의 최대 부분합은 이전 최대 부분합이 반영된 결과값이라는 것이다.

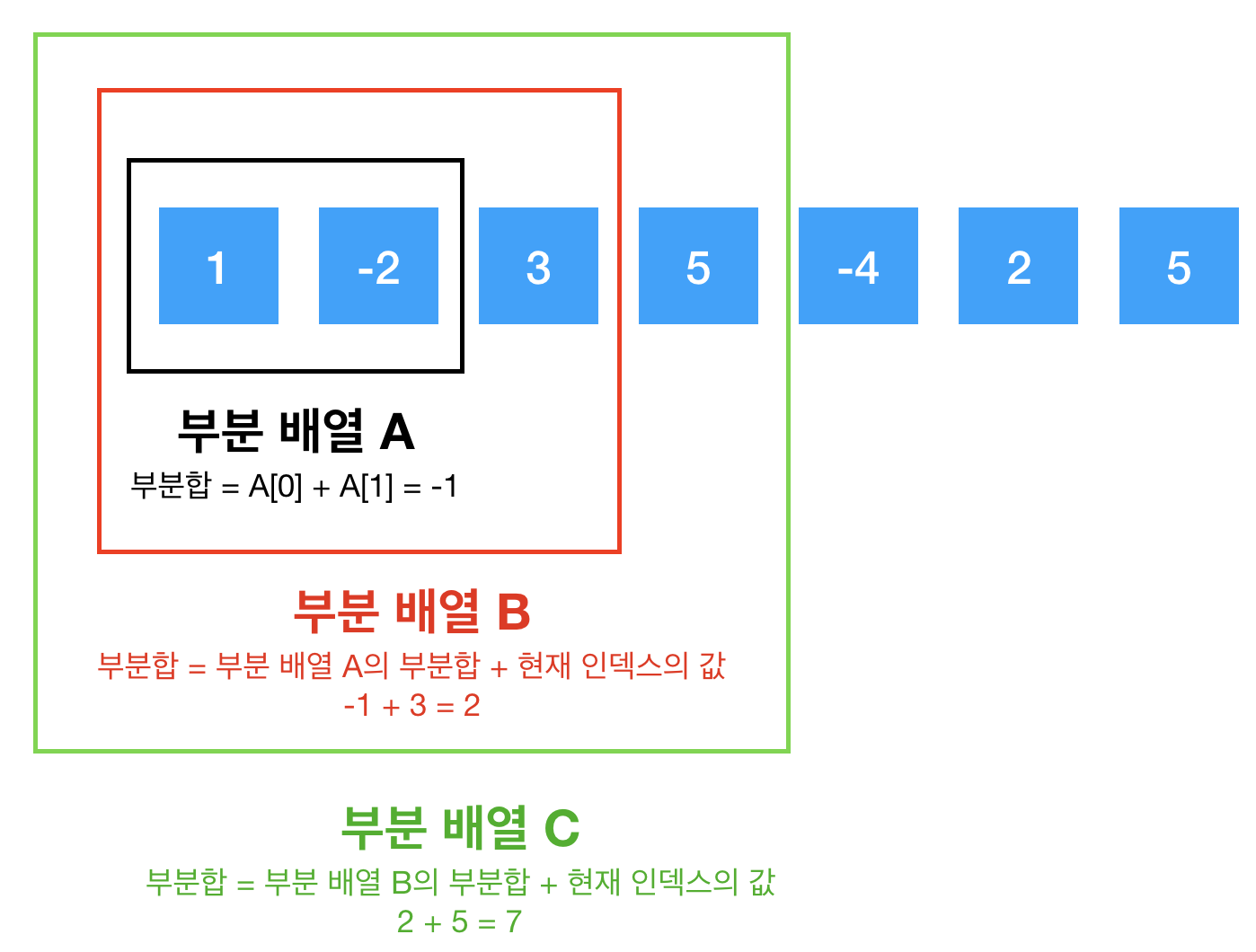
위의 이미지를 보면, 각각의 부분배열의 합은 이전 부분배열의 합에 현재의 인덱스 값을 더한 값임을 알 수 있다.

이를 응용해보면, 이전 인덱스가 가질 수 있는 최대 부분합에 현재의 인덱스 값을 더한다면 현재 인덱스가 가질 수 있는 최대 부분합을 구할 수 있음을 의미한다. 즉, 이전 인덱스가 갖고 있는 최대 부분합을 알고 있다면 현재 인덱스의 최대 부분합을 쉽게 구할 수 있다.

각각의 인덱스가 가질 수 있는 최대 부분합을 구하는 방법은 간단하다. 각각의 인덱스 값은 이전 인덱스가 갖고 있는 최대 부분합을 연장할지, 아니면 자신의 값으로 초기화할지 그저 선택을 하면된다.

최대 부분합을 연장한다는 것은 이전 인덱스의 최대 부분합 값에 현재 인덱스의 최대 부분합 값을 더한 값이 현재 인덱스 값보다 크다는 것을 의미한다.

풀이 코드

var maxSubArray = function(nums) {      for (let i = 1; i < nums.length; i++) {          nums[i] = Math.max(nums[i], nums[i] + nums[i - 1]);      };      return Math.max(...nums); };